light-matter interaction
Overview :
Our system is a one-dimensional interacting spin chain and the atomic medium
is coupled to photon baths at the boundaries as shown in figure below.
We want to describe the photon transport and its interaction with spin-
chains.We here find both transient and steady-state transport properties
of a monochromatic laser light passing through an atomic medium modeled as a Heisenberg-type interacting spin- 1/2 chain.We study several
properties of the system such as reflection coefficients $R(t)$ ,transmission
coefficients $\tau(t)$ at transient state and at steady state. We use the Quantum
Langevin Equation QLE approach to calculate nonlinear light
propagation through one-dimensional (1D) interacting quantum lattice models
connected to photon baths at the boundaries. The QLE approach for nonequilibrium transport
is an extension of
the Heisenberg-Langevin equation approach to nonequilibrium open quantum systems.
System :
We write Quantum Langevin Equation corresponding to the
system and use these to describe the system properties. We first apply the QLE approach
to an atomic medium of two-atoms modeled
as a Heisenberg-type interacting spin- 1/2 chain with nearest-neighbor
coupling. The total Hamiltonian consisting of the atomic medium of two atoms(1),the
photon baths(2,3), and the atom-photon coupling(4,5) terms is :
$$H_T = H_M + H_{LB} + H_{RB} + \nu _{LM} + \nu_{RM}$$
$$H_M = 2 J_x \sigma_1 \sigma_2^{\dagger} + 2 J_x \sigma_1^{\dagger} \sigma_2 +
4J_z \sigma_1^{\dagger}\sigma_1 + \omega_1 \sigma_1^{\dagger}\sigma_1 + \omega_2 \sigma_2^{\dagger} \sigma_2 -----------(1)
$$
$\sigma_i^{\dagger} \& \sigma_i $ are the raising and lowering operators of the $i$th two-level atom.
$$ H_{LB} = \int _{-\infty}^{\infty} \omega_k a_k^{\dagger}a_k dk -----------(2)$$
$$ H_{RB} = \int _{-\infty}^{\infty} \omega_k b_k^{\dagger}b_k dk -----------(3)$$
$a_k^{\dagger},b_k^{\dagger}$ create a photon with wave number $k$, respectively, at left \&right side photon baths
$$H_{LM} = \int _{-\infty}^{\infty} g_L (a_k^{\dagger}\sigma_1 + \sigma_1^{\dagger}a_k) dk ---------(4)
$$
$$H_{RM} = \int _{-\infty}^{\infty} g_R (b_k^{\dagger}\sigma_N + \sigma_N^{\dagger}b_k) dk ---------(5)
$$
The atom-photon coupling strength at left and right sides of the medium are $g_L$ and $g_R$ respectively.
Photon Transport :
We are here interested in getting total transmitted and reflected power which in turn would give transmission and reflection coefficients of light.
The time-dependent transmission and reflection coefficients for an incoming light from the left of the medium.
The time-dependent transmission cocfficients :
$$T(t) = \frac{2\Gamma_R}{\nu_g I_{in}} S_{22}(t)$$
The time-dependent reflection coefficients :
$$R(t) = 1 + \frac{2\Omega_L}{\nu_g I_{in}}+ \frac{2\Gamma _L}{\nu_g I_{in}} S_{11}(t)$$
Transient Properties of Scattered Light :
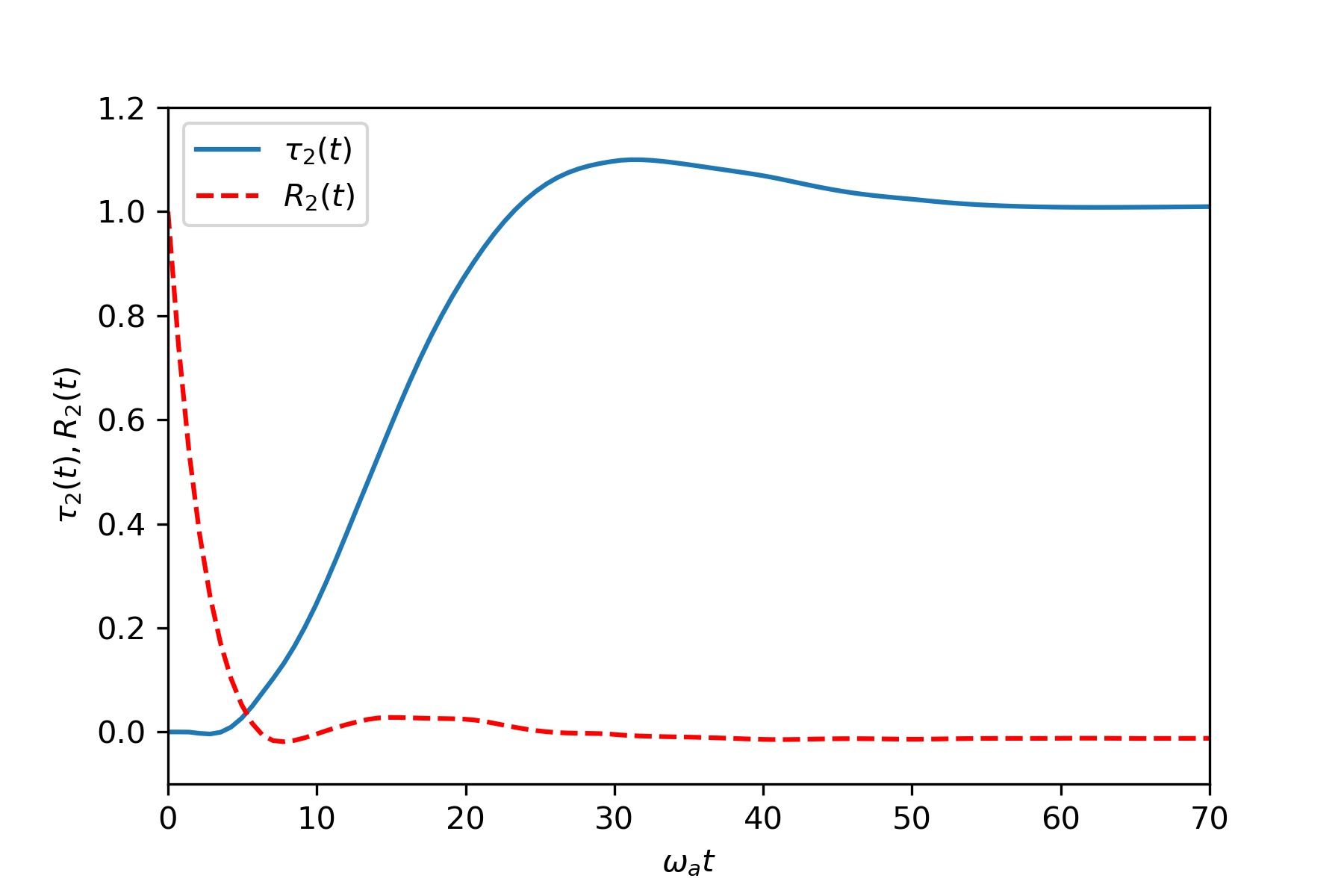
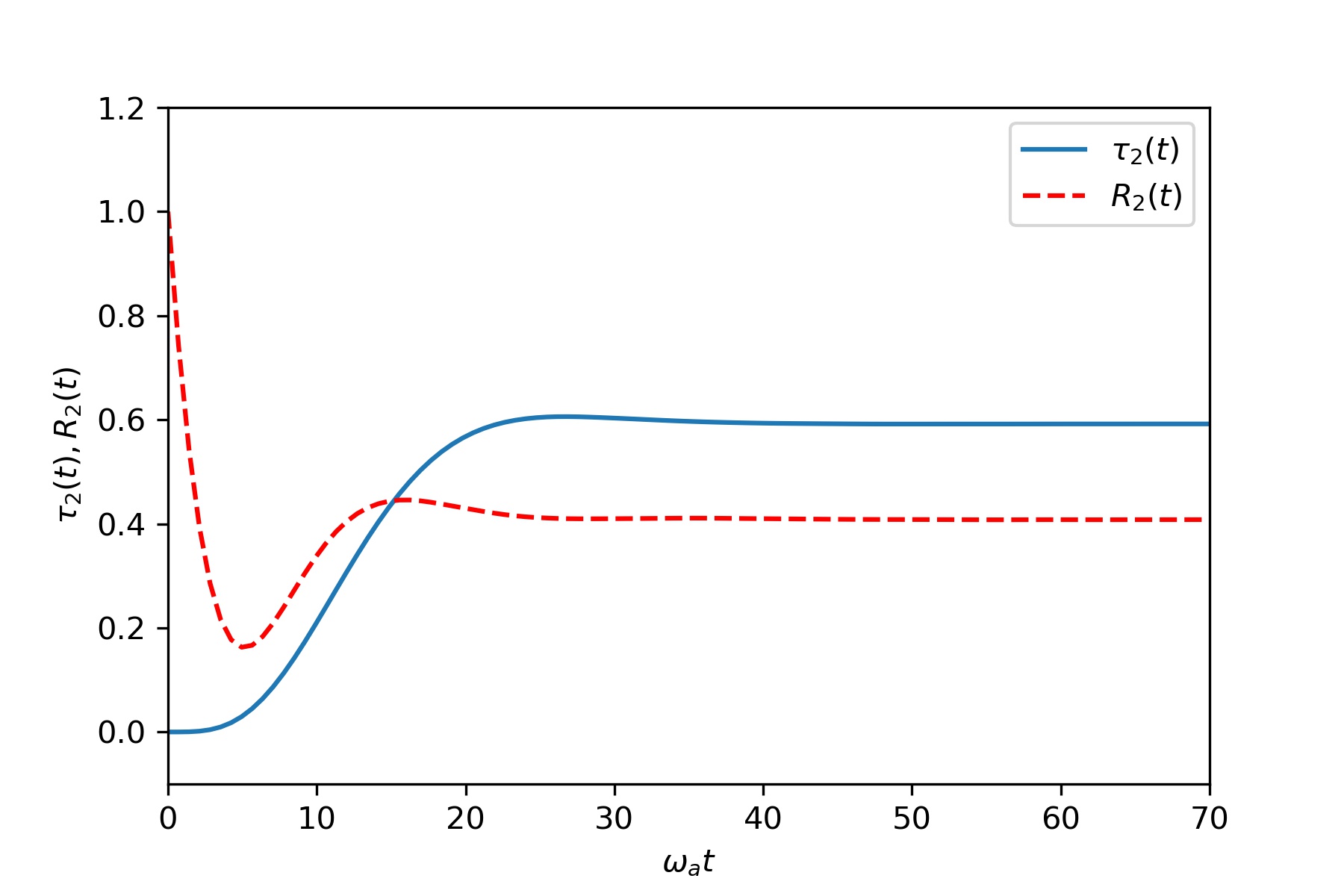
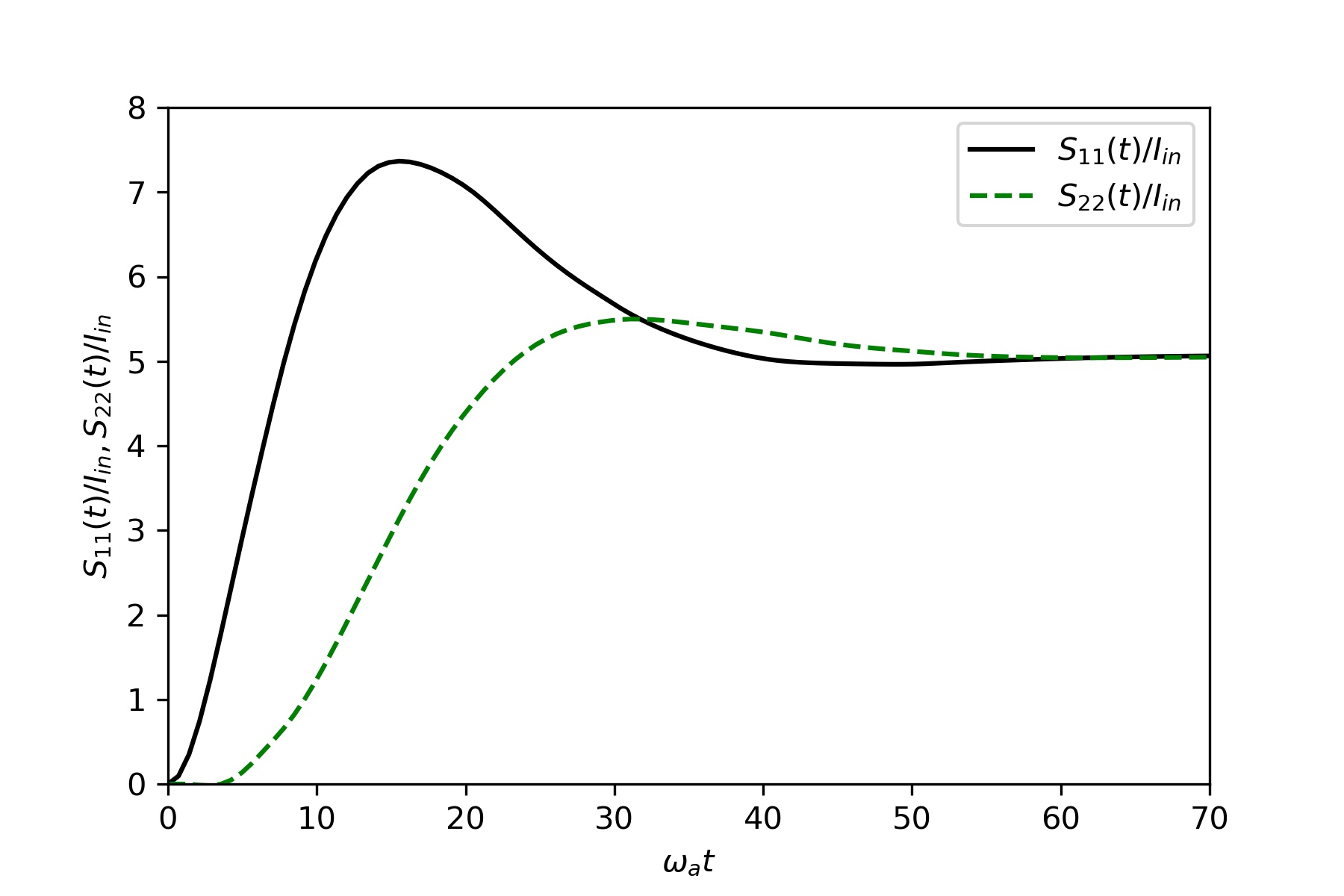
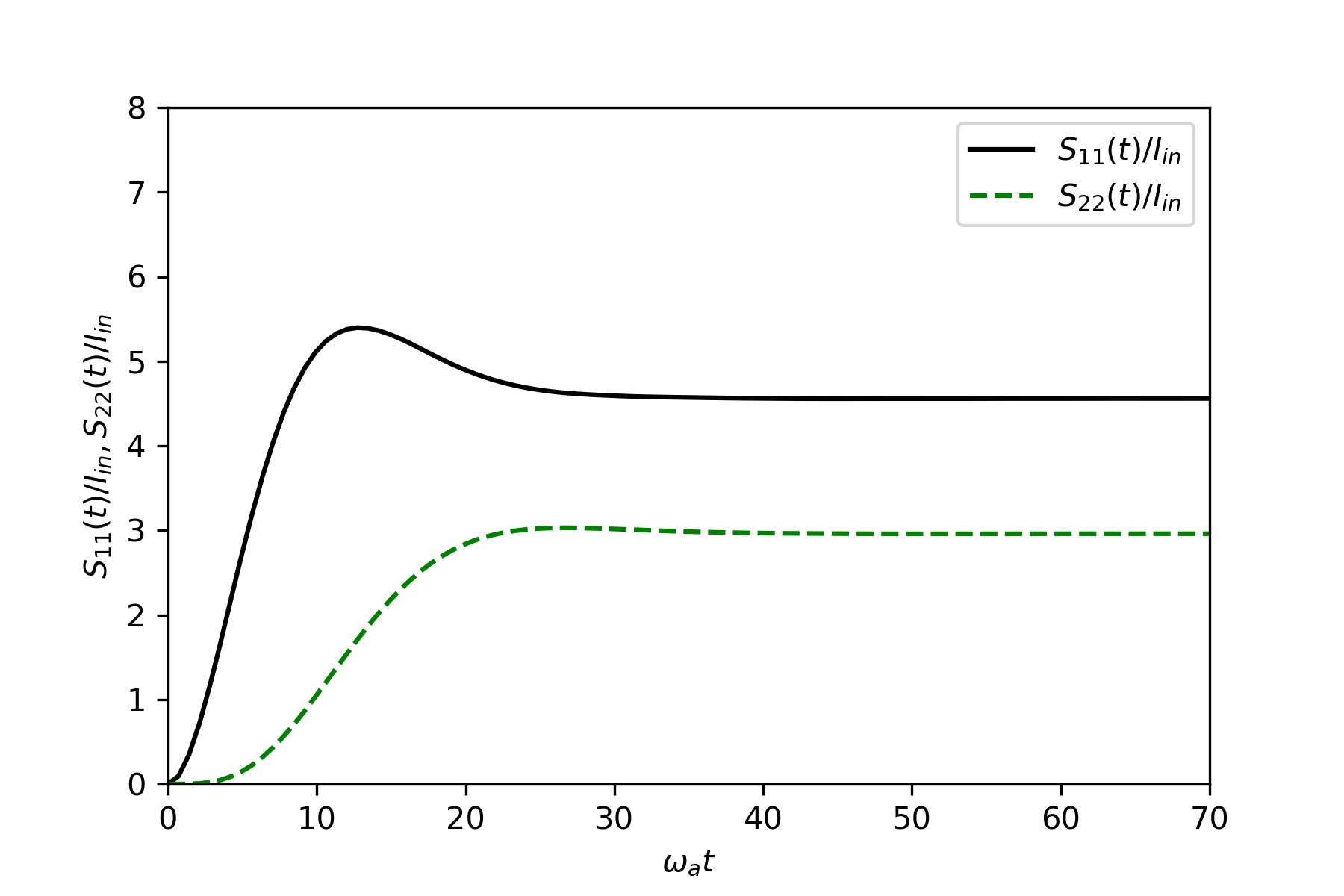
Transient properties of the scattered light and the atoms in a medium of
two atoms driven by a laser light. Figure (1,2) depict time-evolution of
transmission coefficient $\tau(t)$ and reflection coefficient $R(t)$ of a laser
light from the left of the medium modeled as an interacting spin chain.
Figure (3,4) depict time evolution of excited atoms scaled by power of
the incident laser.
The common parameters are
$\omega_1 = \omega_2 = \omega_p = \omega_a, J_x = J_z = 0.05 \omega_a , \Gamma _ L = \Gamma _ R = 0.1 \omega_a $
$I_{in} $ is in units of $\frac{\omega_a}{\nu_g}$
figure 1 : Time-evolution of transmission coefficient $\tau_2(t)$
and reflection coefficient $R(t)$ when $I_{in} = 1.6 x 10^{-5}$
figure 2 : Time-evolution of transmission coefficient $\tau_2(t)$
and reflection coefficient $R(t)$ when $I_{in} = 0.04$
figure 3 : Time evolution of excited atoms scaled by power of the incident laser when $I_{in} = 1.6 x 10^{-5}$
figure 4 : Time evolution of excited atoms scaled by power of the incident laser when $I_{in} = 0.04 $
Steady State Properties :
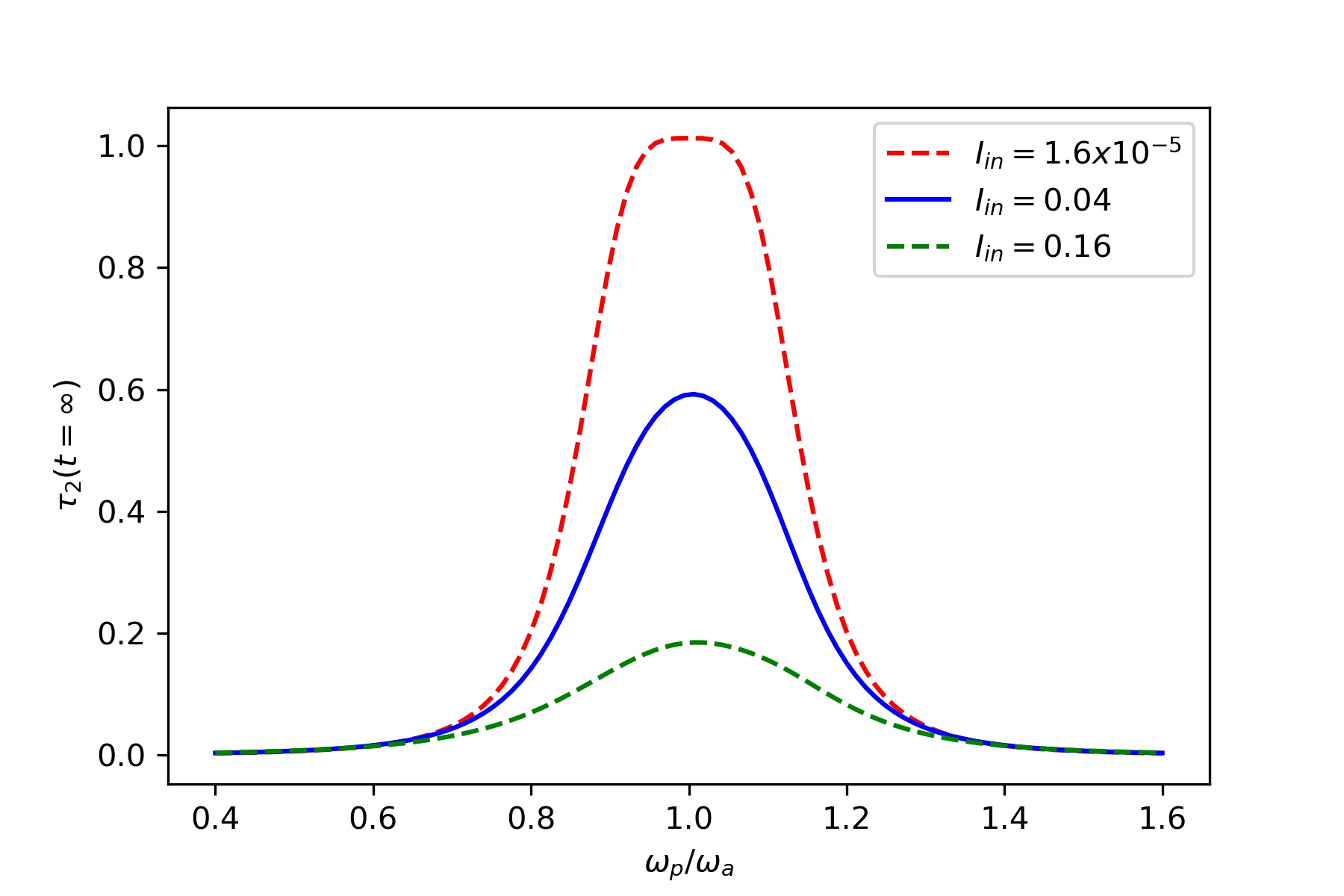
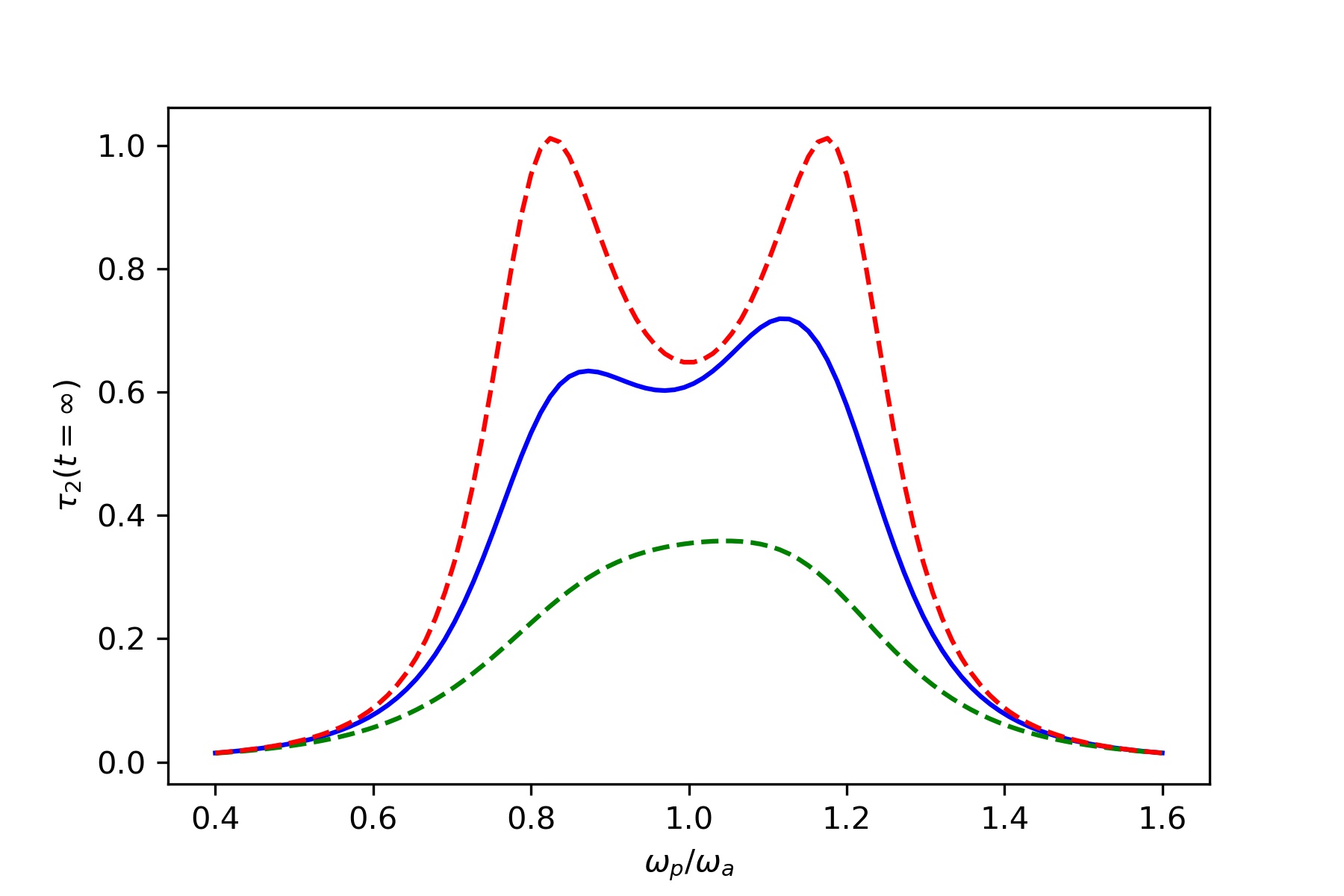
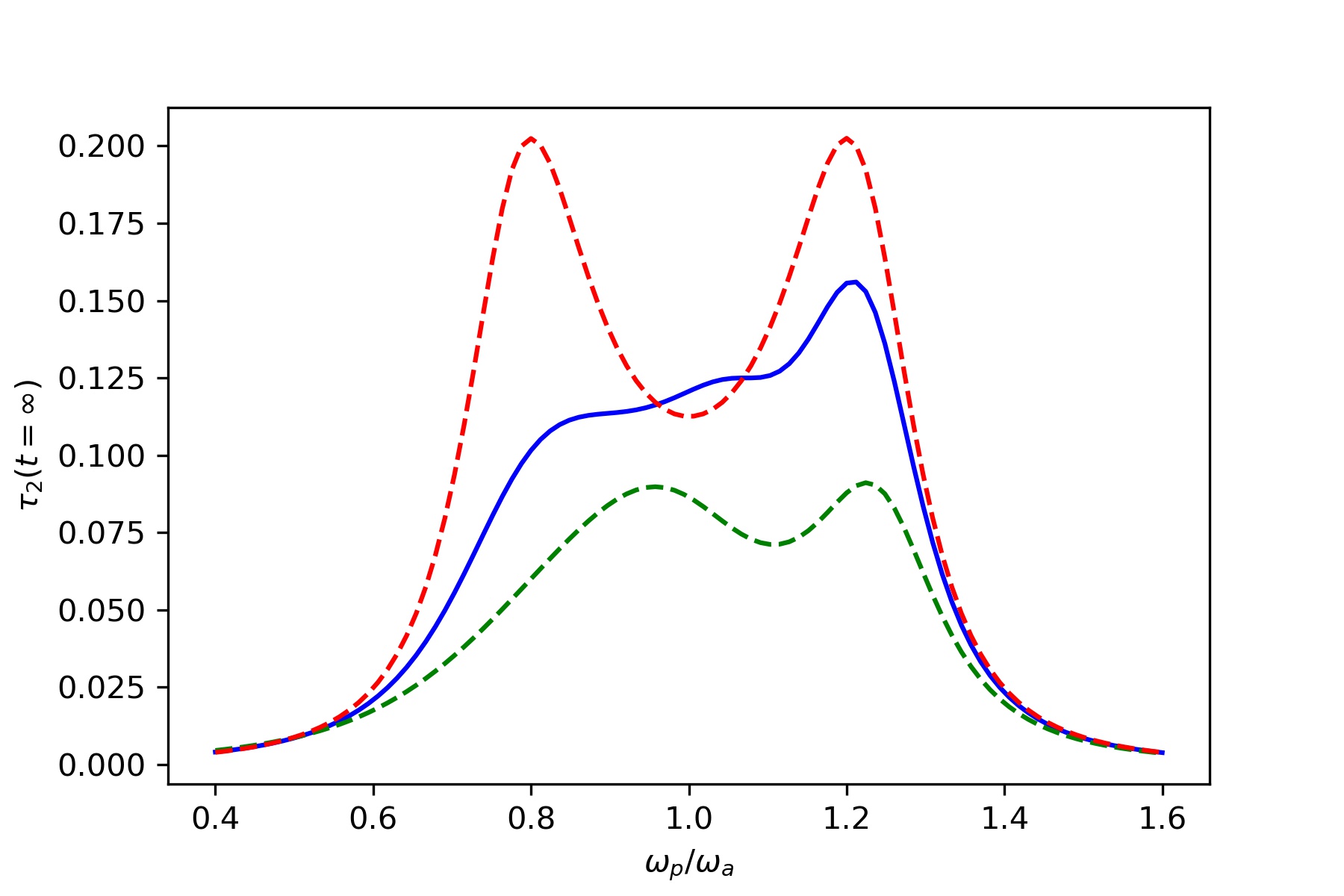
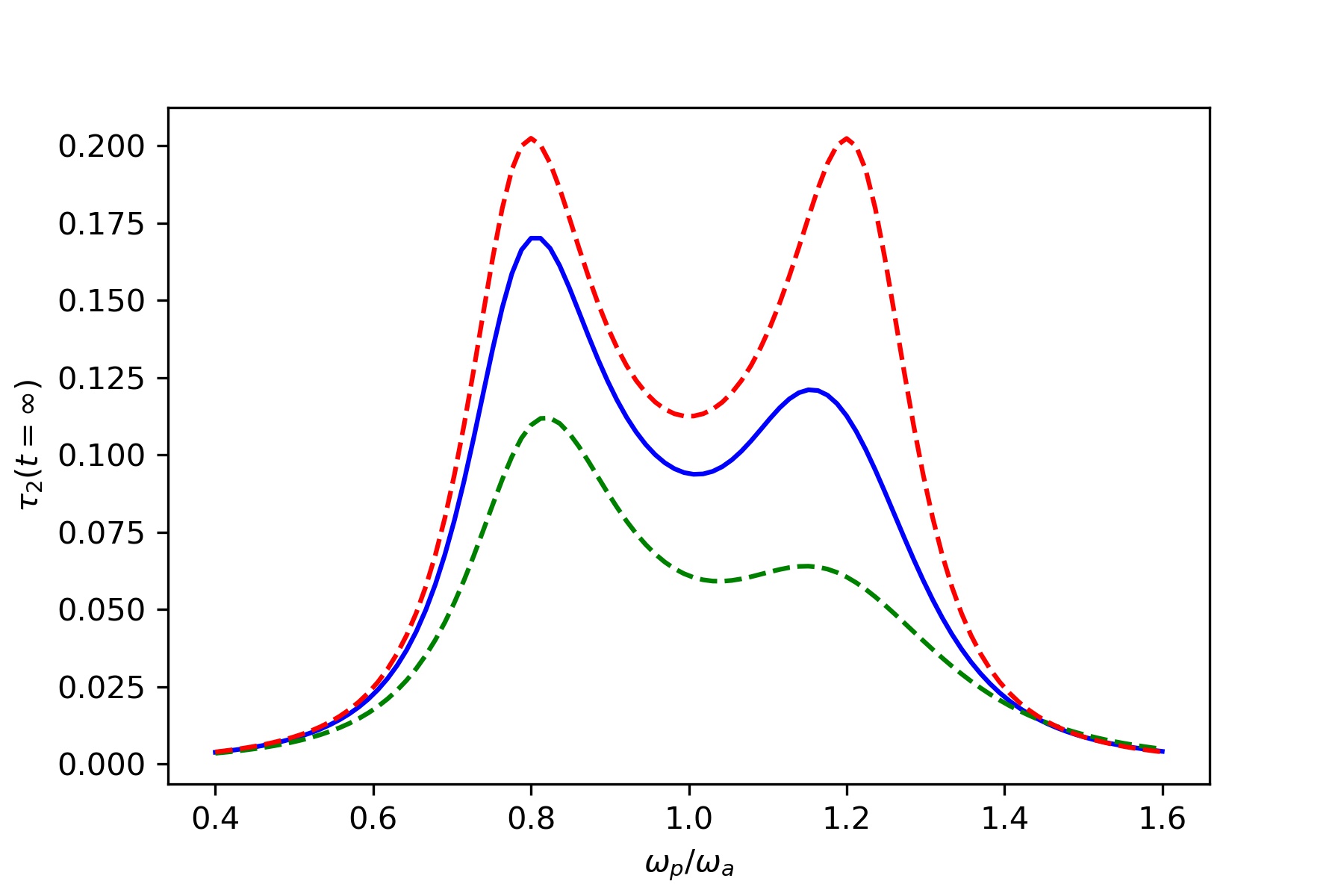
Linear and nonlinear laser transmission through an atomic medium of
two atoms modeled as an interacting spin chain.The steady state
transmission coefficient $\tau_2(t = \infty)$ vs scaled frequency $\frac{\omega_p}{\omega_a}$, of the laser
for various intensities ($I_{in} \propto E_p ^2$) of the incident laser.
In all the plots $\Gamma_L = \Gamma _R = 0.1, J_z, = 0.05.$ The rates $\Gamma_L,\Gamma_R,J_x,J_z$ and
$\omega_1, \omega_2$ are in units of $\omega_a$, and $I_{in}$ is in units of $\frac{\omega}{\nu_g}$.
figure A : $\omega_1=\omega_2=1, J_x = 0.05$
figure B : $\omega_1=\omega_2=1, J_x = 0.1$
figure C : $\omega_1= 0.8, \omega_2 = 1.2, J_x = 0.05$
figure D : $\omega_1= 1.2, \omega_2 = 0.8, J_x = 0.05$
References :
Light propagation through one-dimensional interacting open quantum systems
Pooja Manasi and Dibyendu Roy
Phys. Rev. A 98, 023802